> 1. 树型数据结构的理解与应用
> 2. 树中的深度优先遍历的操作
> 3. 回溯算法的技巧
> 4. 树型的大剪枝和小剪枝
> 5. LinkedList的应用
### 题目
近日,接触到关于组合、子集、排列的算法问题。例如,**第40题** [组合总和Ⅱ](https://leetcode-cn.com/problems/combination-sum-ii),就包含**回溯算法**和**深度优先遍历**以及**剪枝**操作技巧,非常考验计算机思维。这道题到底如何,那就一探究竟。现在给出题目全文:
40.给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
- `1 <= candidates.length <= 100`
- `1 <= candidates[i] <= 50`
- `1 <= target <= 30`
```
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
```
```java
class Solution {
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
}
}
```
### 分析
仔细读题,题目说给定一个集合,从中找出所有可能的组合数字组成目标和。
题目有2个显性要求:
- 一是每个数字只能使用一次,不能重复使用;
- 二是解集不能包含重复的组合;
- 但是也有一个隐性要求,这个集合candidates中数字是可以重复的。
对于这道题也可以理解为**几数之和**问题。如果有解决 **第 15 题**([三数之和](https://leetcode-cn.com/problems/3sum/))、 **第 47 题**([全排列 II](https://leetcode-cn.com/problems/permutations-ii/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liwe-2/))、 **第 39 题**([组合之和](https://leetcode-cn.com/problems/combination-sum/))的经验,理解和分析这道题就会很简单。
那么现在就开始分析!
解决这道题就是穷举所有解,而这些解集可以用树形结构呈现。如下图所示。

> 看起来就像是DFS(Depth First Search,深度优先遍历,简称 DFS)的实现!
例如,这就展示出数组`[1,2,3]`所有的排列组合`[[],[1],[2],[3],[1,2],[1,3],[2,3],[1,2,3]]`。

那么解这道题,就可以利用树型树结构的特点进行思考分析。**如果把根节点作为第 0 层,将每个节点和根节点之间树枝上的元素作为该节点的值,那么第 `n` 层的所有节点就是大小为 `n` 的所有子集**。节点存放所有的解集(包括根节点,根节点存放空集。)
那么对于本题的条件限制(组合中有重复的数字,但要求数字只能使用一次,并且解集不能重复),则需要绘画出如下的树型结构图。


仔细观察上图和分析本例,`candidates=[2,5,2,1,2],target = 5`。在本例中,先将数组排序得到`candidates=[1,2,2,2,5]`;先列出所有不重复的解集,即实现深度优先遍历。由于每个数只能使用一次,因此深层结点可以考虑的分支数会越来越少。在树型结构中呈现出左半部分叶子节点深,右半部分叶子节点浅。再来考虑重复的部分,对于同一个结点产生的分支,边上减去的数相同的分支,只保留第一个分支。怎么理解这句话,在本例中,有3个2。对于`5`这个结点,有3个`减去2`的分支,减去的数相同,那么只保留第一个分支。剩余的2个分支无论后续叶子结点如何都已经不重要,因为剩余2个分支的组合肯定包含在第一个分支的组合中。也可以说,剩余2个分支的组合是第一个分支组合的真子集。更加详细的说,第一个分支的候选集合为{1,2,2,2,5},剩余2个分支的候选集合分别为{1,2,2,5}、{1,2,5}。那么第一个分子的候选集合产生的组合肯定包含剩余2个分支的候选集合产生的组合。
对于这一种减去数相同并且多余的分支,直接减掉,没有往下搜索的必要,直接pass。
要是实现这一过程,在代码中实现为
```java
// 小剪枝:同一层相同数值的结点,从第 2 个开始,候选数更少,结果一定发生重复,因此跳过,用 continue
if (i > begin && candidates[i] == candidates[i - 1]) {
continue;
}
```
理解了这一步,剩下的工作变得很简单啦。接下来就是“大剪枝”,也就是减去红色的叶子节点的那一分支。在代码中的实现就是判断`target-candidates<0`
```java
// 大剪枝:减去 candidates[i] 小于 0,减去后面的 candidates[i + 1]、candidates[i + 2] 肯定也小于 0,因此用 break
if (target - candidates[i] < 0) {
break;
}
```
那么我们最后需要什么样的结果?即`target==0`,在代码中实现为`target-candidates[i]=target`(也就是递归),具体实现为:
```java
if (target == 0) {
res.add(new ArrayList<>(path));
return;
}
```
然后配合使用回溯算法。那么回溯算法是什么呢?
其实回溯算法其实就是我们常说的 DFS 算法,本质上就是一种暴力穷举算法。
废话不多说,直接上回溯算法框架。**解决一个回溯问题,实际上就是一个决策树的遍历过程**。你只需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
回溯算法框架:
```java
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
```
不理解没有关系,在后面配合代码会一起讲解。
### 代码实现
现给出全部代码:
```java
/**
* @author Zhoujiankang
*/
public class CombinationSum2 {
//存放结果
List<List<Integer>> res = new LinkedList<>();
// 存放路径
LinkedList<Integer> track = new LinkedList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
int len = candidates.length;
// 关键步骤
Arrays.sort(candidates);
backtrack(candidates, len, 0, target, track, res);
return res;
}
private void backtrack(int[] candidates, int len, int start, int target, LinkedList<Integer> track, List<List<Integer>> res) {
if (target == 0) {
res.add(new ArrayList<>(track));
return;
}
for (int i = start; i < len; i++) {
// 大剪枝:减去 candidates[i] 小于 0,减去后面的 candidates[i + 1]、candidates[i + 2] 肯定也小于 0,因此用 break
if (target - candidates[i] < 0) {
break;
}
// 小剪枝:同一层相同数值的结点,从第 2 个开始,候选数更少,结果一定发生重复,因此跳过,用 continue
if (i > start && candidates[i] == candidates[i - 1]) {
continue;
}
track.addLast(candidates[i]);
// 因为元素不可以重复使用,这里递归传递下去的是 i + 1 而不是 i
backtrack(candidates, len, start + 1, target - candidates[i], track, res);
track.removeLast();
}
}
}
```
在这个框架实现中,满足条件是target减去集合中某些数后,target为0,在代码中表现为`target==0`。如果你有解决 **第 15 题**([三数之和](https://leetcode-cn.com/problems/3sum/))的经验就会明白,想一想`(nums[0]+nums[1]+...+nums[n-1])==target`与`target-nums[0]-....-nums[i]==0`这两个表达式在计算机中的计算量分别是多少?(考虑最坏的情况,不考虑其他因素,前者的工作量是后者的(n-1)/2倍。)即使它们表达的含义是一样的。
简单来说,对于计算机而言,只要判断目标值减去元素值之间的差值是否为0 ,如果大于0,则就减下一元素值;小于0,则就放弃这个元素值。
所以这便是计算机思维的独特之处!
最后,`backtrack` 函数开头看似没有 base case,会不会进入无限递归?
其实不会的,当 `start == nums.length` 时,叶子节点的值会被装入 `res`,但 for 循环不会执行,也就结束了递归。
### 扩展
#### 1.想一想为什么要使用LinkedList?而不使用ArrayList?
答:这就要仔细分析Array(数组)与LinkedList(链表)这两种数据结构的特点。
- **数组(Array)** 是一种很常见的数据结构。它由相同类型的元素(element)组成,并且是使用一块连续的内存来存储。
我们直接可以利用元素的索引(index)可以计算出该元素对应的存储地址。
数组的特点是:**提供随机访问** 并且容量有限。
```
假如数组的长度为 n。
访问:O(1)//访问特定位置的元素
插入:O(n )//最坏的情况发生在插入发生在数组的首部并需要移动所有元素时
删除:O(n)//最坏的情况发生在删除数组的开头发生并需要移动第一元素后面所有的元素时
```
- **链表(LinkedList)** 虽然是一种线性表,但是并不会按线性的顺序存储数据,使用的不是连续的内存空间来存储数据。
链表的插入和删除操作的复杂度为 O(1) ,只需要知道目标位置元素的上一个元素即可。但是,在查找一个节点或者访问特定位置的节点的时候复杂度为 O(n) 。
使用链表结构可以克服数组需要预先知道数据大小的缺点,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但链表不会节省空间,相比于数组会占用更多的空间,因为链表中每个节点存放的还有指向其他节点的指针。除此之外,链表不具有数组随机读取的优点。
```
假如链表中有n个元素。
访问:O(n)//访问特定位置的元素
插入删除:O(1)//必须要要知道插入元素的位置
```
答案已经很明显,在回溯算法的实现中,我们更多是对元素的插入、删除操作。如`res.add(new ArrayList<>(track));`、`track.addLast(candidates[i]);`、` track.removeLast();`。简单来说,如果使用ArrayList而不使用LinkedList,那么复杂度扩大`n`倍。但也要注意相比ArrayList,LinkedList会占用更多的空间。
#### 2.时间复杂度是多少?空间复杂度是多少?
时间复杂度:O(n)。其中 n 是数组candidates 的长度。在大部分递归 + 回溯的题目中,我们无法给出一个严格的渐进紧界,故这里只分析一个较为宽松的渐进上界。
空间复杂度:O(n)。除了存储答案的数组外,我们需要 O(n) 的空间存储列表track,以及递归的栈。
#### 3.如果增加条件,如仅仅需要集合K个元素,组成组合。
(同样地,不能包含重复解集,每个元素只能使用一次。)那么代码怎么实现?
提示:仅仅需要K个元素,就是树的高度,或者第K层。
参考第 77 题「 [组合](https://leetcode-cn.com/problems/combinations)」,这道题就迎刃而解。这是第77题的实现代码。
```
List<List<Integer>> res = new LinkedList<>();
// 记录回溯算法的递归路径
LinkedList<Integer> track = new LinkedList<>();
// 主函数
public List<List<Integer>> combine(int n, int k) {
backtrack(1, n, k);
return res;
}
void backtrack(int start, int n, int k) {
// base case
if (k == track.size()) {
// 遍历到了第 k 层,收集当前节点的值
res.add(new LinkedList<>(track));
return;
}
// 回溯算法标准框架
for (int i = start; i <= n; i++) {
// 选择
track.addLast(i);
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(i + 1, n, k);
// 撤销选择
track.removeLast();
}
}
```
答案:
关键代码
```java
private void backtrack(int[] candidates,int k, int len, int start, int target, LinkedList<Integer> track, List<List<Integer>> res) {
if (target == 0 || k == track.size()) {
res.add(new ArrayList<>(track));
return;
}
```
### 总结
以下这习题,无论怎么变化,增加多少限制条件,其核心就是利用回溯算法解决。回溯算法很好利用递归高效率,同时也非常考验计算机思维。
[78. 子集(中等)](https://leetcode-cn.com/problems/subsets)
[90. 子集 II(中等)](https://leetcode-cn.com/problems/subsets-ii)
[77. 组合(中等)](https://leetcode-cn.com/problems/combinations)
[39. 组合总和(中等)](https://leetcode-cn.com/problems/combination-sum)
[40. 组合总和 II(中等)](https://leetcode-cn.com/problems/combination-sum-ii)
[216. 组合总和 III(中等)](https://leetcode-cn.com/problems/combination-sum-iii)
[46. 全排列(中等)](https://leetcode-cn.com/problems/permutations)
[47. 全排列 II(中等)](https://leetcode-cn.com/problems/permutations-ii)
另外,在[37. 解数独(困难)](https://leetcode-cn.com/problems/sudoku-solver)中,非常适用于回溯算法解决。还有一点,良好使地用数据结构,会显著提高实现效率。
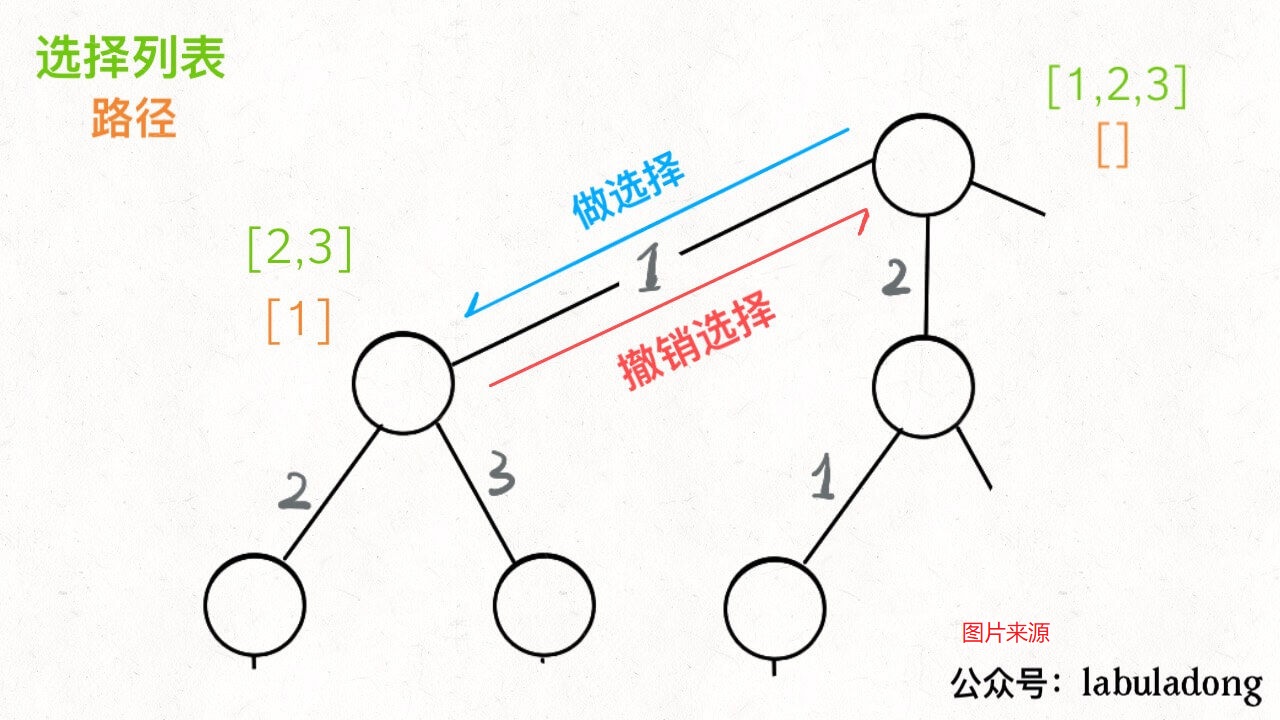
在【组合】、【子集】、【排列】问题中回溯算法的实现



